Math Says Don't Slow Down At Red Lights

(You can also read this post on Substack (with worse LaTeX formatting in this case), where you can sign up for email subscriptions if you'd like.)

The Problem

One day, probably like ten years ago, I was riding my bike to high school as I approached a red light, unsure of when exactly it would turn green, and noticed I was trying to slow down at some steadily decreasing rate. I was trying to simultaneously accomplish two things:

• Slow down as little as possible, in order to preserve as much speed as possible and spare my lazy legs
• Slow down enough to make sure that the light will turn green before I reach the intersection and have to come to a complete stop

So I was basically trying to do an optimization, balancing these two factors. It occurred to me that there must be some optimum solution that I should be able to reach mathematically, given some assumptions. The solution could be obvious to some people, but to me it really wasn’t clear; maybe you should avoid the brakes entirely in order to maintain the maximum possible speed if you get lucky and the light turns green quickly, or maybe you should brake significantly in order to delay reaching the intersection and ensure that you can maintain at least some speed if you get unlucky and the light stays red for a long time.

Formalizing this optimization problem:

• \(v(t)\) is the speed as a function of time. It must be monotonically decreasing, since you want to conserve energy until you’re sure that you can pass the intersection in a green light. This only describes the speed before the light turns green; after that, our optimization puzzle is done, the solution is very clear. The cyclist should not slow down at all, and probably should start speeding up again.
• \(T\) is the maximum time a light at this intersection can stay red. We assume the cyclist knows this from previous encounters with this intersection.
• \(t_g\) is the amount of time that passes from the cyclist’s first sight of the red light until it turns green, assumed to be drawn randomly from a uniform distribution between \(0\) and \(T\). The cyclist does not know \(t_g\), and has to find a strategy for the distribution of possibilities.
• \(D\) is the initial distance to the stoplight.
• \(V=v(0)\) is the initial speed.

First, we can handle an easy case. If \(V < D/T\), then you’re guaranteed to see a green light before you reach the intersection, and you should not touch your brakes at all. From now on, we will assume this is not the case.

Expected Value Of Speed

So, if we want to preserve as much speed as possible, we might want to maximize the expected value of the final speed when the light turns green. This expected value will be calculated by using an integral to average the final speed over all possibilities for the unknown value \(t_g\):

Expected final speed when the light turns green: \(\frac{1}{T}\int_0^T v(t_g) dt_g\)

However, we now note that this integral is exactly equal to the expression which calculates the total distance traveled at time \(T\)! So, we just need an \(v(t)\) that maximizes distance traveled at time \(T\). Given our assumption \(V > D/T\), we know it is possible to have a \(v(t)\) function that reaches \(D\) at time \(T\) (the function which stays at \(v=V\) until you reach the intersection and then comes to an abrupt halt at \(v=0\)). So, \(\int_0^T v(t_g) dt_g=D\) is possible. And \(\int_0^T v(t_g) dt_g>D\) is forbidden, because that means you plan to enter the intersection even if the light is red. Therefore, we’ve found our optimum!

So, this is our answer. It’s totally inconsequential what you do with your brakes, just make sure you reach the intersection before you’re 100% sure the light will turn green. So, you can do lots of different braking patterns, and they will all lead to the same tiredness in your legs at the end of the day. Or do they…

On second thought, maximizing the expected value of speed isn’t really the problem we initially set up. I really care about the tiredness in my legs, not the speed of my bike. And the tiredness in my legs is determined (roughly) by energy consumption, not speed.

This would be our solution if going from 10 to 20 mph was exactly as easy as going from 0 to 10 mph. This is actually the case for rockets, where a certain amount of fuel gives you a certain amount of Delta-v (change in velocity), and kinetic energy doesn’t really matter (kinetic energy isn’t the intuitive quantity to use for rockets in flight because the ejected rocket fuel has different kinetic energy depending on what reference frame you’re considering).

So if our bike was in space, this would be the right answer! But this is not the right answer for any propulsion method where you gain speed by pushing on a surface or fluid, as is the case for a bike, and basically everything else on earth.

Expected Value Of Kinetic Energy

Really, we care about how much energy we lose when braking, and the corresponding amount of energy we’ll need to re-add by pedaling once we pass the light. This means we want to maximize the expected value of our kinetic energy, which is proportional to the square of our speed. Specifically, we have this problem:

Find \(v(t)\) that maximizes \(\int_0^T \left[v(t)\right]^2 dt\) (the expected value of the kinetic energy \(\frac{1}{2} m v^2\) for some constant mass \(m\)) subject to \(\int_0^T v(t) dt = D\) (we will want to get all the way to the stop light by the time we’re 100% sure it will turn green) and \(v(0)=V\) (we start out with a certain initial speed).

This is a harder problem than the one we just solved, and will take more work to reach a proof of an optimal solution.

Failed Solution #1

This integral doesn’t directly work out to a nice physical quantity that we already know like in the previous case. So instead, we’ll try to use calculus of variations, the field of math that tries to find optimal functions to solve some problem.

Let us phrase our problem in the typical language of the Calculus of variations, with an action functional \(s[v]\) and a Lagrangian \(L\):

\[s[v] = \int_0^T L(t, v, \dot{v}) dt\] \[L(t, v, \dot{v}) = v^2\]

Now, let’s apply the Euler-Lagrange equation, guaranteed to give us the local extrema of \(s[f]\).

\[\frac{\partial L}{\partial v} - \frac{d}{dt}\frac{\partial L}{\partial \dot{v}} = 0\] \[2 v - 0 = 0\] \[v = 0\]

Well, I guess \(v(t)=0\) and \(S[v]=0\) is a true minimum, and therefore a local extremum, so this did work. However, we failed to include our boundary condition \(v(0)=V\), so this is useless for our problem.

Failed Solution #2

Building off Failed Solution #1, we can note that we have a distance constraint that we have not used, \(\int_0^T v(t) dt = D\) (at the you certainly don’t want to be short of the intersection at the last moment the light could turn green, you certainly don’t want to be short of the intersection, and you certainly don’t want to go into the intersection).

Using \(\int_0^T v(t) dt = D\), we can add zero to our equation for the action, using a Lagrange multiplier \(\lambda\):

\[s[v] = \int_0^T L(t, v, \dot{v})dt + \lambda \left(\int_0^T v(t) dt - D\right)\]

Then, combining the integrals:

\[s[v] = \int_0^T \left(L(t, v, \dot{v}) + \lambda v \right)dt - \lambda D\]

\(\lambda D\) is a constant term which will have no impact on our variational equations, so we can consider just the integral term:

\[\int_0^T \left(v^2 + \lambda v \right)dt\]

Now, we can apply the Euler-Lagrange equation again, while including this new term:

\[\frac{\partial}{\partial v}\left(v^2 + \lambda v \right) - \frac{d}{dt}\frac{\partial}{\partial \dot{v}} \left(v^2 + \lambda v \right) = 0\] \[2v + \lambda - 0 = 0\] \[v = -\lambda/2\]

So our Euler-Lagrange equation tells us that the velocity should be constant. Using our distance constraint, this gives us \(v(t)=D/T\). However, this does not match our initial condition \(v(0)=V\), since we are assuming \(V>D/T\)! So this solution still can’t be correct.

Correct Solution

I actually only started writing this post because I thought I had found an interesting application of Euler-Lagrange equations (initially an even more incorrect solution featuring a time-varying Lagrange multiplier). But it turns out that the actual solution is not differentiable, so it cannot be found by calculus of variations using these methods. To explain, I’ll have to resort to a slightly more hand-wavy but still correct geometric argument.

One way to think about this problem is in terms of the area enclosed by the \(v(t)\) vs \(t\) graph. This area corresponds to the final distance to the light \(D\), which must be our trajectory in the case that the light does not turn green early and \(t_g=T\). We can think about how to manipulate this constant area when optimizing our trajectory. Here are three examples of the types of equal-area \(v(t)\) vs \(t\) plots we can consider:

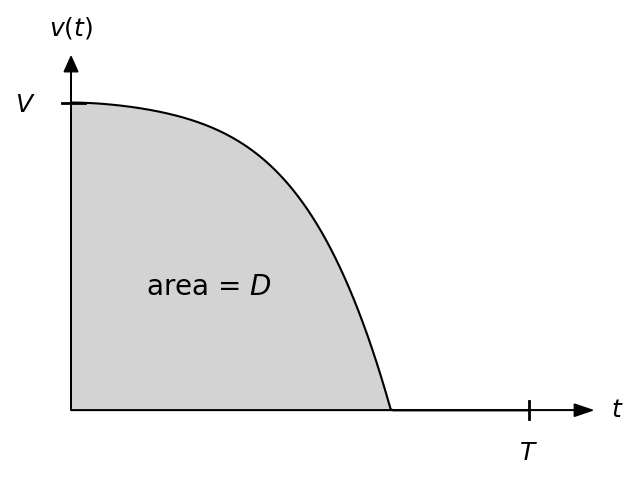
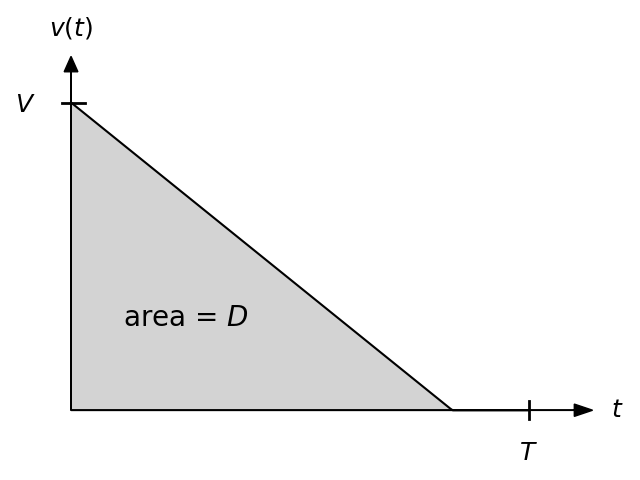
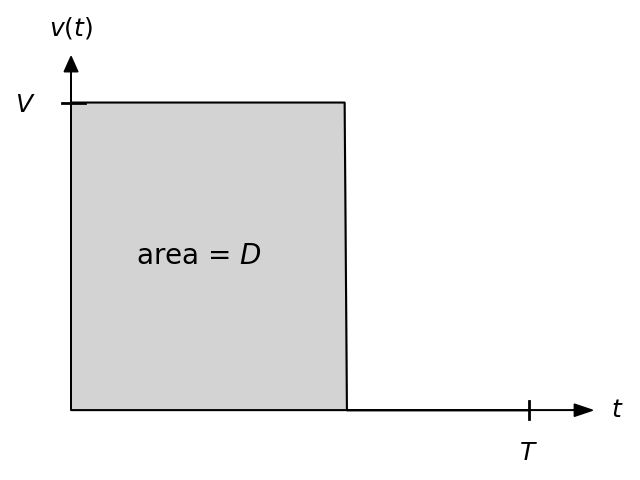
Going back to the expected value of speed, this corresponds to the average height of the \(v(t)\) graph between \(t=0\) and \(t=T\). Since the area is constant, the average height is constant, which again agrees with our earlier conclusion that it does not matter what \(v(t)\) you choose or how hard you brake.

For the expected value of kinetic energy, this corresponds to the average squared height of the \(v(t)\) graph between \(t=0\) and \(t=T\). Squaring a large value is more valuable than squaring multiple small values (for example \((2x)^2>x^2+x^2\)), so we want to maximize the time we can square our maximum initial speed. So, the solution is the third drawing above, a step function which keeps the maximum speed as long as possible, and slams on the brakes right when you reach the intersection (if the light hasn’t turned green yet). We can see that failed Solution #2 gave us a hint of the correct solution, indicating contant velocity, but not describing the sudden stop once you have traveled to the intersection.

So, apparently you’re not supposed to slow down at a stoplight! You should keep off the brakes as much as possible, hoping to zoom through the intersection at full speed with a green light, but ready to slam on the brakes as hard as you can at the last second if you’re unlucky and the light stays red too long. Good to know!

Should I Really Not Slow Down At Red Lights?

Keep in mind that I’m not telling you you shouldn’t brake, I’m just telling you that math is telling you you shouldn’t brake. In reality, you should consider safety and whatnot and slow down before reaching the intersection. This math tells you that you’ll save some energy, but at the same time, other math will tell you that this method will increase wear on your brakes and tires, will likely make you come to a complete stop where balancing or stepping off your pedals can be annoying, and is relatively likely to cause injury or death to yourself or others.

You need to decide for yourself how you’ll balance this tradeoff between energy efficiency and human life. For myself, I’ll probably brake a little bit harder than I would have before knowing this, but nothing too crazy. Human intuition about how you should behave is actually pretty great at taking all of these factors into account, so I probably wasn’t really far off from the true optimum all along.